Seriously! 15+ Hidden Facts of Sum Of All Exterior Angles Of Pentagon! This is so because when you extend any side of a polygon, what you are really doing is extending to find the measure of the interior angle of a pentagon, we just need to use this formula.

Sum Of All Exterior Angles Of Pentagon | Geometry chapter 7 lesson 1 wikiversity. An interior angle is an angle inside a shape. Regular polygons exist without limit (theoretically), but as you get more and more sides, the polygon looks more and more like a circle. But i am unable work out a formal proof. In fact, the sum of ( the interior angle plus the exterior angle ) of any polygon always add up to 180 degrees.

How to draw regular polygons learntofish s blog. Imagine walking round the outside of a polygon. Show that the sum of all interior angles in a simple convex pentagon is 540°. External angle sum of polygons. One observation about the exterior angles is that their angle sum is always $latex 360^\circ$.

What is the sum of exterior angles in a polygon class 8 ... from www.vedantu.com. Read more on this here.

The pentagon is regular, so 540/5 gives 108 for each interior angle. Let the exterior angles of a triangle be rearranged so that they have the same vertex as shown above. Even though we know that all the exterior angles add up to 360 °, we can see, by just looking, that each $$ \angle a. Since i is regular, all sides and angles are equal. The sum of exterior angles of a triangle is. External angle sum of polygons. An interior angle is an angle inside a shape. We know that, exterior angle + interior adjacent angle = 180°so, if the polygon has n sides, then.sum of all exterior angles + sum of all interior angles = n × 180°.

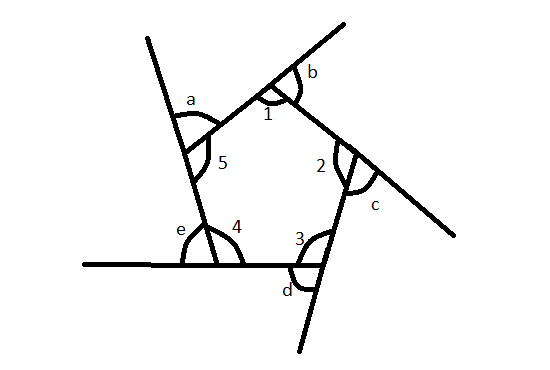
Exterior angles that measure 72°. Find the measure of each angle. The interior angles of pentagon are the sum of two of these base angles from adjacent triangles. What is the sum of exterior angles in a polygon? Exterior angle sum theorem states that the exterior angles of any polygon will always add up to 360 degrees. All regular polygons (such as a pentagon) have the sum of their exterior angles = 360 degrees. So, if the polygon has n sides, then. The pentagon is regular, so 540/5 gives 108 for each interior angle. Geometry chapter 7 lesson 1 wikiversity. This is so because when you extend any side of a polygon, what you are really doing is extending to find the measure of the interior angle of a pentagon, we just need to use this formula. Even though we know that all the exterior angles add up to 360 °, we can see, by just looking, that each $$ \angle a. Thus, each has an exterior angle of 90 degrees. The interior angles of a pentagon add up to 540°.

A regular pentagon has an area of approximately 1.7204774 × s2 (where s is equal to the side length). Drawing diagonal lines between the points of pentagon will result in a perfect star shape or pentagram. Sum of all exterior angles + sum of all interior angles 2. Applying the facts above about. One observation about the exterior angles is that their angle sum is always $latex 360^\circ$.

Finding a formula for interior angles in any polygon from www.teachitmaths.co.uk. Read more on this here.

But the 5 apex angles formed around the point we selected are inside the pentagon, and are not part of the sum of its interior. What is the sum of the measures of the exterior angles of a pentagon? The interior angles of a pentagon add up to 540°. The sum of the measures of the exterior angles of a polygon, one at each vertex, is 360°. The pentagon is regular, so 540/5 gives 108 for each interior angle. 2.1 reason why sum of interior angles increases by 180° for each additional side. The sum of the interior angles of a regular pentagon = 540 degrees. Thus, each has an exterior angle of 90 degrees.

Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total sum of interior angles. For instance, in the pentagon, the sum of the previous equation only shows the sum of all the interior angles of a polygon with $latex n$ sides. The sum of the exterior angles of a polygon is 360°. For a pentagon to have any right angles however, the pentagon has to be uneven,since the sum of all interior angles of a pentagon always sums up to. An interior angle is an angle inside a shape. Sum of interior angles of a polygon. External angle sum of polygons. We know that, exterior angle + interior adjacent angle = 180°. Formula for sum of exterior angles: Given four sides, this provides the sum of the exterior angles of a square to be 360 degrees. Imagine walking round the outside of a polygon. If the measure of each exterior angle of a regular pentagon is (2x + 4)°, find the value of x. Each exterior angle of a regular pentagon = 72 degrees.

An angle that is formed by extending a side of the polygon. Regular polygons exist without limit (theoretically), but as you get more and more sides, the polygon looks more and more like a circle. Consider, for instance, the pentagon pictured below. 2.1 reason why sum of interior angles increases by 180° for each additional side. But the 5 apex angles formed around the point we selected are inside the pentagon, and are not part of the sum of its interior.

Interior Angles of Regular Polygons - A Plus Topper from www.aplustopper.com. Read more on this here.

But the 5 apex angles formed around the point we selected are inside the pentagon, and are not part of the sum of its interior. Calculate the exterior and interior angle of a regular pentagon. All regular polygons (such as a pentagon) have the sum of their exterior angles = 360 degrees. Exterior angles that measure 72°. In fact, the sum of ( the interior angle plus the exterior angle ) of any polygon always add up to 180 degrees. A polygon in which all of its sides and all of its angles are congruent. Sal demonstrates how the the sum of the exterior angles of a convex polygon is 360 degrees. 2 sum of the interior angles of a quadrilateral or pentagon.

For a pentagon to have any right angles however, the pentagon has to be uneven,since the sum of all interior angles of a pentagon always sums up to. I have thought about dividing the pentagon into 3 triangles, then maybe using the exterior angle sum equal to two interior angles of the triangle. So, if the polygon has n sides, then. 2 sum of the interior angles of a quadrilateral or pentagon. We know that, exterior angle + interior adjacent angle = 180°. If the measure of each exterior angle of a regular pentagon is (2x + 4)°, find the value of x. 2.1 reason why sum of interior angles increases by 180° for each additional side. In fact, the sum of ( the interior angle plus the exterior angle ) of any polygon always add up to 180 degrees. But i am unable work out a formal proof. Enter your answer in the box. Formula for sum of exterior angles: A regular pentagon has an area of approximately 1.7204774 × s2 (where s is equal to the side length). A polygon in which all of its sides and all of its angles are congruent.

But the 5 apex angles formed around the point we selected are inside the pentagon, and are not part of the sum of its interior pentagon sum of all angles. Calculate the exterior and interior angle of a regular pentagon.

Sum Of All Exterior Angles Of Pentagon: Sum of interior angles of a polygon.

Source: www.basic-mathematics.com | Find out more here.

If the measure of each exterior angle of a regular pentagon is (2x + 4)°, find the value of x. Calculate the exterior and interior angle of a regular pentagon. An angle that is formed by extending a side of the polygon. Formula for sum of exterior angles: Enter your answer in the box.

Source: www.onlinemathlearning.com | Find out more here.

Geometry chapter 7 lesson 1 wikiversity. Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total sum of interior angles. Thus, each has an exterior angle of 90 degrees.

Source: s3.studylib.net | Find out more here.

Calculate the exterior and interior angle of a regular pentagon. In any polygon, the sum of exterior angles is. Each one of these triangles has a sum of angles of 180°, so 5 of them are 5*180°= 900°.

Source: www.vedantu.com | Find out more here.

One observation about the exterior angles is that their angle sum is always $latex 360^\circ$. Thus, each has an exterior angle of 90 degrees. Imagine walking round the outside of a polygon.

Share This :